Money for glass or money for the wind

The principle of reasonable sufficiency applies in daily life when solving every day issues. It is also relevant when choosing glass structures. For many years, their thermal characteristics have been neglected, mainly due to a lack of regulation tools. It was obvious that two layers of glass in a frame are better than one. And if the gaps are properly sealed, there won't be any drafts from the window.

Later, fencing structures based on PVC and aluminum systems with thermal breaks appeared. This is where the difficulties of choice arose. And when the option of using three or four layers of glass with energy-efficient coatings of various purposes emerged: energy-saving, sun-protective, multifunctional (combining summer and winter features), special (conductive, self-cleaning, anti-condensation, etc.), chaos became even greater.

Representatives of glass and glass processing companies offer options for insulated glass units for various purposes, ranging from industrial, commercial, and office buildings to the segment of PVC windows for civil construction and housing renovation. At the same time, some specific features of double-glazed windows and different types of glass are sometimes concealed from customers. These features later become the cause of complaints, dissatisfaction, and defects that hinder the further use of the product.

In this article, we will try to understand the concept of lensing, or the change in the plane of glass in insulated glass units. This phenomenon is typical for most translucent structures with a fragment area exceeding 4 m². In structures with smaller fragmentation, it is less noticeable and generally does not create the same issues observed in large and medium-format glazing.

How does lensing occur?

The effects of “lensing” or, in worse cases, "implosion" — the compression of glass in insulated glass units — are directly related to the climatic load applied to them. This involves an increase or decrease in gas pressure within the glass unit compared to the initial pressure set during manufacturing. The change in gas pressure is associated with temperature variations in the surrounding environment and barometric pressure fluctuations. The influence of pressure change with altitude can be disregarded due to its minimal impact.

During the manufacturing process, the interior of the glass unit is sealed with dried air or inert gas at the appropriate levels of atmospheric pressure and temperature. These parameters constantly change during usage, leading to the appearance of internal loads within the glass unit, which deform the glass to a greater or lesser extent. The most significant factor is temperature variation. Since the unit is airtight, the gas expands inside the sealed volume when heated, increasing the pressure. As a result, the glass unit becomes convex. During cooling, the internal pressure decreases, causing the glass unit to compress or even “collapse.”

An example of a significant change in the interpane space due to a relatively small temperature decrease in a double-glazed unit is shown in Figure 1.

The change in internal volume is related to internal pressure and can be described by the Mendeleev-Clapeyron equation. The load resulting from gas expansion or compression is perceived in two ways simultaneously. Part of the load is borne by the glass through direct resistance to deformation, while another part is compensated by the change in gas volume through glass deformation.

In other words, to calculate the deflection of the glass, it is necessary to determine which part of the internal load will be compensated by the change in gas volume and which part will be directly absorbed by the glass.

How to calculate the load on the glass of an insulated glass unit?

To calculate the load, let's consider two extreme cases as ideal models:

1. The glass fully absorbs the internal load if it is perfectly rigid, following Charles's law for ideal gases (isochoric process).

2. The internal load is fully compensated by volume change if the glass is perfectly flexible, following Gay-Lussac's law (isobaric process).

The actual case should be calculated as an intermediate between these ideal models.

In the first case, let's assume that there is an internal load, q, acting on the layers of glass within the unit. Considering that the volume of the glass unit remains constant in this case, the internal load q corresponds to the absolute difference between atmospheric pressure and the pressure inside the glass unit, ∆Рмах. It can be expressed as:

In the second case, the internal pressure q cannot be supported in the double-glazed unit by flexible walls, and due to the deformation of the walls, it will immediately be transformed into a change in the internal volume ΔV. Since such a model can only have a change in volume, this change in ΔV is equal to the maximum ΔVмах. Let's express this by the formula:

In reality, when both methods of perception of the internal load are involved, it can be mathematically expressed through the equilibrium equation:

The change in internal volume ΔV is a function of the glass deflection ΔV(f), and the glass deflection f is a function of the load f(q). Therefore, this equilibrium equation allows iterative determination of the value of the internal pressure q.

Let's introduce the following designations:

• Рв – pressure in the glass unit chamber at the time of production.

• Тв – gas temperature in the glass unit chamber at the time of production (°К).

• Vв – volume of the glass unit chamber at the time of production.

• Ре – pressure in the glass unit chamberduring operation.

• Те – gas temperature in the glass unit chamber during operation (°К).

• Vе – volume of the glass unit chamber during operation.

Then, according to Gay-Lussac's law: ΔVмах = Vв*(Те/Тв-1).

And according to Charles's law: ΔVмах  = Рв*(Те/Тв-1).

Now we just need to determine the value of the temperature inside the glass unit chamber, Те.

We propose considering two methods.

Method 1: Listen to the recommendations of leading experts in the field of translucent constructions. In particular, apply the formula suggested by Mrs. O. Kurenkova, Director of the National Institute of Window Systems.

Tе = (Твул + Твн) / 2,

where:

Твул – outside air temperature (street temperature).

Твн – inside air temperature.

Method 2: Calculate the temperature using the formula provided in document СН 481-75 "Instruction for the design, installation, and operation of glass units." This document is no longer valid as it was relevant during the time of the Soviet Union, and new regulations determining the temperature inside sealed units have not been adopted. Therefore, the formula is as follows:

Tе = k*Твул + (1-k) * Твн ,

where k is a coefficient equal to 0.39 for single-glazed units and 0.26 for double-glazed units.

The results of the calculation using Method 2 for a single-glazed unit are shown in Figure 2.

Let's calculate the specific values

Let's attempt the calculation using Method 2 as the basis. For example, let's take the following data:

• Gas temperature in the sealed unit at the time of production Тв = +18°C.

• Outside air temperature Твул = -20°C.

• Inside air temperature Твн = +20°C.

Then:

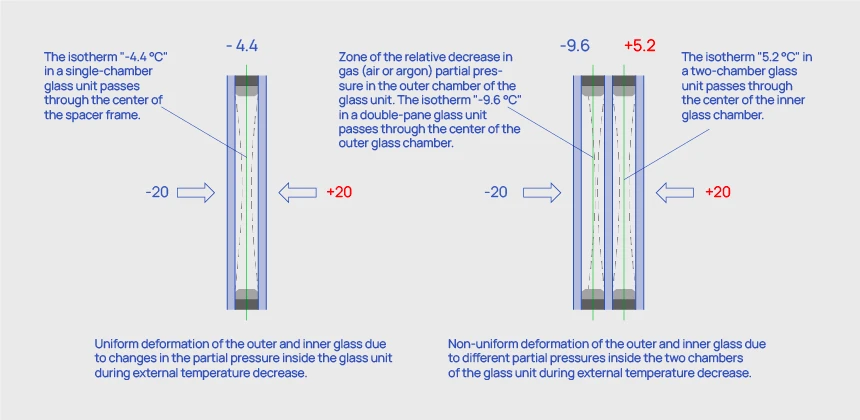
• Isotherm of the middle part of the gas in a single-glazed unit chamber during operation:

Те = 0,39 * 20 - (1-0,39) * 20 = -4,4 °C.

• Isotherm of the middle part of the outer chamber of a double-glazed unit during operation:Те = 0,26 * 20 - (1-0,26) * 20 = -9,6 °C

• Isotherm of the middle part of the inner chamber of a double-glazed unit during operation: Те = (-9,6 + 20) / 2 = 5,2 °C.

For a single-glazed unit with dimensions of 3 x 2 m2 and a spacer distance of 16mm, we obtain:

• ΔVмах = Vв*(Те/Тв - 1) = -7,39 liters (initial volume = 96 liters).

For a double-glazed unit with dimensions of 3 x 2 m2 and two spacer distances of 16mm, we obtain:

• For the outer chamber: ΔVмах = Vв * (Те/Тв - 1) = -9.105 liters (initial volume = 96 liters).

• For the inner chamber: ΔVмах = Vв*(Те/Тв - 1) = -4.223 liters (initial volume = 96 liters).

How to prevent glass bending?

After our calculations, we concluded that the volume loss due to gas cooling inside the double-glazed unit is nearly twice as high as a single-glazed unit. This is expected. However, the distribution of volumes within the chambers is uneven. As a result, the volume loss in the outer chamber is over two times higher than in the inner chamber and almost a quarter higher than in a single-glazed unit. A significant change in volume leads to increased glass bending, which causes lensing in the glass units.

Suppose the rigidity characteristics of the glass do not correspond to the loads caused by the loss of partial pressure inside the glass unit. In that case, there is a high probability that the glass will deform, leading to the collapse of the sealed unit. A clear sign of this is the presence of interference rings, known as Newton's rings, in the contact zone between the glass. They occur when light reflects from two surfaces, one of which is flat and the other has a relatively large radius of curvature, making contact with the first surface.

For large-sized insulated glass units and significant temperature differentials, ranging from +20°C to -20°C, the performance of double-glazed units decreases due to the reduction of the interpane space in the first chamber, which leads to a decrease in convective processes within the chamber. These processes are responsible for the heat exchange inside the chamber, ensuring a relative temperature averaging throughout the volume of the glass unit. It also leads to a sharp increase in heat transfer from the middle to the outer glass, causing localized cooling of the central part of the sealed unit. The heat transfer from a hotter body to a cooler one depends quadratically on the distance between the bodies. In other words, by reducing the distance from 16mm to 5mm (i.e., three times), we would experience a nine-fold increase in heat loss.

You might ask, why all this discussion? What can be done to prevent such phenomena?

There are several options available.

For large glass formats, when there is a possibility of a significant reduction in the thermal performance of a double-glazed unit, one option is to use glass with increased thickness for the outer chamber. The increased rigidity of this glass compensates for the load caused by pressure changes within the chamber. Another option is to use a single-glazed unit with enhanced energy efficiency. Additionally, reinforcing the perimeter of the first chamber of the sealed unit using the technology developed by Aestech can greatly increase the unit's stiffness.

The first method is relatively straightforward, but let's delve into the details of the second and third methods.

One or two chambers in a glass unit – which is better?

With the introduction of translucent structures of flat glass with multifunctional thermal coatings, the thermal performance of a single-glazed unit has come close to that of a basic double-glazed unit. Using an online glass unit configurator, we compared the energy-efficient single-glazed unit with a double-glazed unit.

As seen from the calculation, under ideal conditions, the two glass units are almost identical in terms of thermal performance for energy preservation during the winter period. However, the single-glazed unit outperforms the double-glazed unit in terms of solar protection. This is without considering the potential reduction in the interpane space in the double-glazed unit.

What are the implications of installing a double-glazed unit? It involves choosing a different, wider, and stronger profile (a double-glazed unit is one-third heavier and almost twice as wide). It requires reinforcing structural elements in brackets to support the facade system. It complicates installation and increases logistical risks.

We are by no means advocating for replacing all double-glazed units with single-glazed units, especially in the case of small formats where the double-glazed unit has a competitive edge. However, when using large-scale glazing, we recommend conducting structural and thermal calculations to choose translucent structures that will provide the necessary visual and operational characteristics for the facade system.

Another option, which we believe is one of the most effective methods for improving the visual and thermal performance of facade systems, is the use of insulated glass units with higher stiffness developed by Aestech. On the one hand, they allow for the reduction of glass thickness, significantly minimizing the lensing effect and making it practically invisible to the eye. On the other hand, they eliminate most of the structural aluminum elements that contribute negatively to the thermal performance of the facade system due to aluminum's high thermal conductivity.

The correct choice of glazing system must optimize one-time and operational costs for translucent structures so that the "Money for glass" formula works, rather than the "Money for the wind" formula.

AR&D (Analytical Research and Development) Aestech